分数应用题解题思想介绍

〔分析与解〕这题也是从余下的数量来考虑，即，A＋B

＝（100－4O）＝6O（元）→＝A＋B＝（6O÷5）＝12（元）

12×7＝84（元）		×7＝“1”→B
		×7＝→A

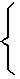A：(100－84)÷(1－×7)＝72（元）

B：100－72＝28（元）

五、合并思想

合并思想就是把题中的两个或两个以上的已知条件合并起来，通过合并，将知识重新组合、分析、比较、归纳，从而找到解题捷径。合并思想包括“量”合并和“率”合并。

1．量合并：量合并就是先把题中的两个或两个以上的已知数量，根据一定的需要直接加起来，然后再思考列式求得答案。

例1．买甲、乙两种商品共6O件，付人民币1260元，如果交换两种商品的件数共付人民币1140元，已知甲商品的价格是乙商品价格的1倍，求两种商品的单价？

[分析与解]由题意得：甲每件商品比乙贵。由交换得：甲商品在交换前比交换后的件数要多，即：甲的件数＞乙的件数。不妨我们设甲原来有X件，乙原来有y件。

（1）甲（x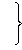）		甲60件	乙（y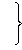）		乙60件	1260元
（2）甲（y）			乙（x）			1140元

1260＋1140＝24OO（元）

将上面的条件（1）和（2）合并起来列式得：

（1260＋1140）÷6O＝（4O元）→甲乙单价和

以及乙：4O÷（l＋1）＝15（元）

    甲：15×1＝25（元）

2．率合并：率合并就是先将题目中的两个或两个以上的分率合并起来，从中得出总数量与总分率之间的关系，然后再借助假设或还原思想求得答案。

例2．甲、乙两件商品，甲的和乙的共值56元，而甲的和乙的共值49元，求甲、乙两件商品的价格？

[分析与解］因为甲乙前后分率正好进行了交换，通过合并可以得到相同的总分率，由此获得解题途径。

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13]  下一页