用等量代换求面积教案

www.dbk123.com小学频道搜集整理了用等量代换求面积教案，供大家参考，希望对大家有所帮助!

用等量代换求面积教案

在组合图形中，除了多边形外，还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，为了计算它们的面积，常常需要变动图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形。就是在多边形的组合图形中，为了计算面积，有时也要用到割补的方法。

例1求下列各图中阴影部分的面积：

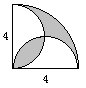
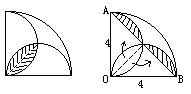
分析与解：(1)如左下图所示，将左下角的阴影部分分为两部分，然后按照右下图所示，将这两部分分别拼补在阴影位置。可以看出，原题图的阴影部分等于右下图中AB弧所形成的弓形，其面积等于扇形OAB与三角形OAB的面积之差。

π×4×4÷4-4×4÷2=4.56。

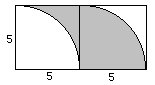
(2)在题图虚线分割的两个正方形中，右边正方形的阴影部分是半径为5的四分之一个圆，在左边正方形中空白部分是半径为5的四分之一个圆。

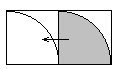
如下图所示，将右边的阴影部分平移到左边正方形中。可以看出，原题图的阴影部分正好等于一个正方形的面积，为5×5=25。

例2在一个等腰三角形中，两条与底边平行的线段将三角形的两条边等分成三段(见右图)，求图中阴影部分的面积占整个图形面积的几分之几。

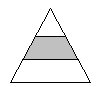
分析与解：阴影部分是一个梯形。我们用三种方法解答。

(1)割补法

从顶点作底边上的高，得到两个相同的直角三角形。将这两个直角三角

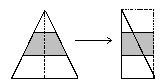
(2)拼补法

将两个这样的三角形拼成一个平行四边形(下页左上图)。

积和平行四边行面积同时除以2，商不变。所以原题阴影部分占整个图形面

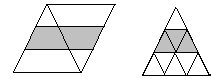
(3)等分法

将原图等分成9个小三角形(见右上图)，阴影部分占3个小三角形，

注意，后两种方法对任意三角形都适用。也就是说，将例题中的等腰三角形换成任意三角形，其它条件不变，结论仍然成立。

例3如左下图所示，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。求这个梯形的面积。

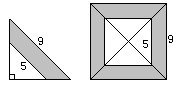
分析与解：因为不知道梯形的高，所以不能直接求出梯形的面积。可以从等腰直角三角形与正方形之间的联系上考虑。将四个同样的等腰直角三角形拼成一个正方形(上页右下图)，图中阴影部分是边长9厘米与边长5厘米的两个正方形面积之差，也是所求梯形面积的4倍。所以所求梯形面积是(9×9-5×5)÷4=14(厘米2)。

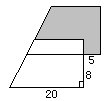
例4在左下图的直角三角形中有一个矩形，求矩形的面积。

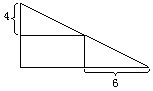
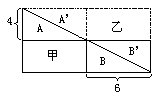
例5左下图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC的面积。

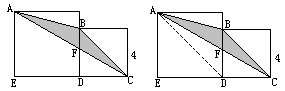
分析与解：这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系。连结AD(见右上图)，可以看出，三角形ABD与三角形ACD的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等。因为三角形AFD是三角形ABD与三角形ACD的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABF与三角形 FCD面积仍然相等。根据等量代换，求三角形ABC的面积等于求三角形BCD的面积，等于4×4÷2=8(厘米2)。

练习21

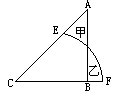
1.左下图中，等腰直角三角形ABC的腰为10厘米，以C为圆心、CF为半径画弧线EF，组成扇形CEF。如果图中甲、乙两部分的面积相等，那么扇形所在的圆的面积是多少?

[1] [2]  下一页